Let’s understand the concept of per unit system by solving an example. In the one-line diagram below, the impedance of various components in a power system, typically derived from their nameplates, are presented. The task now is to normalize these values using a common base.
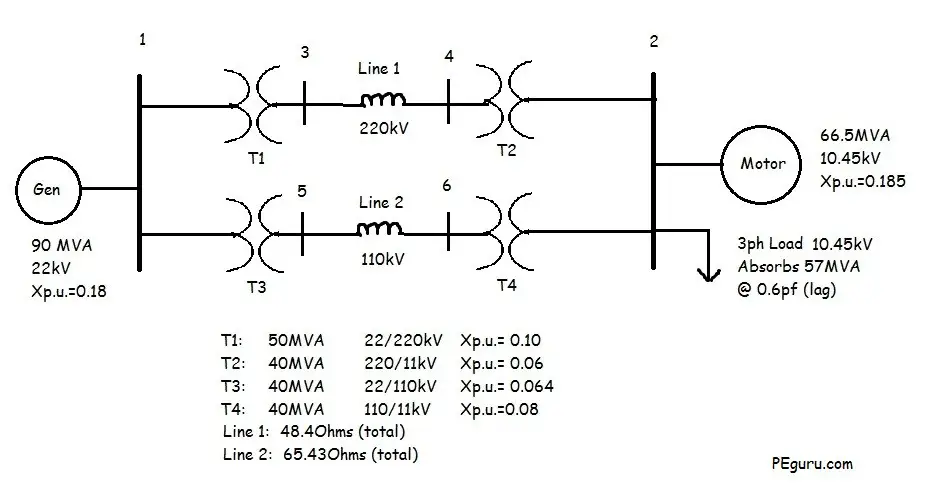
Now that you have carefully examined the system and its parameters, the equivalent impedance diagram for the above system would look something like the following.
Resistive impedance for most components have been ignored. Rotating machines have been replaced with a voltage source behind their internal reactance. Capacitive effects between lines and to ground are ignored as well.
To obtain the new normalized per unit impedances, first we need to figure out the base values (Sbase, Vbase, Zbase) in the power system. Following steps will lead you through the process.
Step 1: Assume a system base
Assume a system wide S_{base} of 100MVA. This is a random assumption and chosen to make calculations easy when calculating the per unit impedances.
So, S_{base} = 100MVA
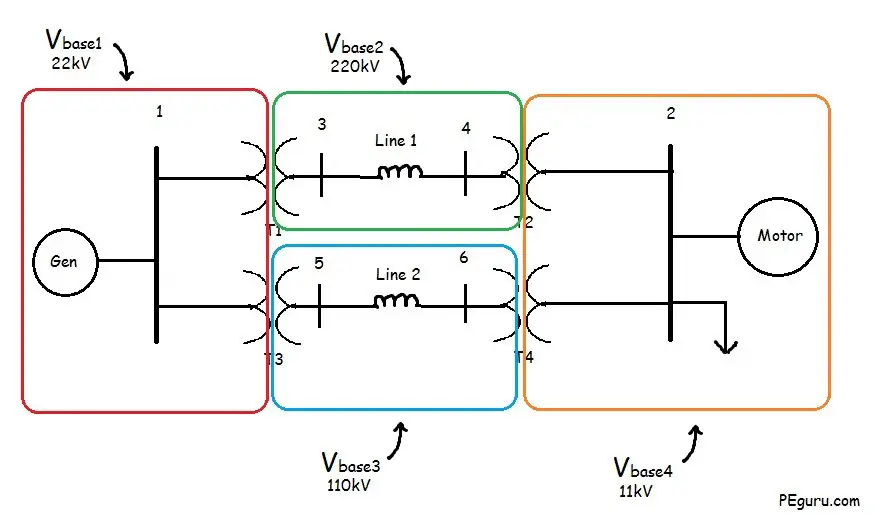
Step 2: Identify the voltage base
Voltage base in the system is determined by the transformer. For example, with a 22/220kV voltage rating of T1 transformer, the V_{base} on the primary side of T1 is 22kV while the secondary side is 220kV. It does not matter what the voltage rating of the other components are that are encompassed by the V_{base} zone.
See figure below for the voltage bases in the system.
Step 3: Calculate the base impedance
The base impedance is calculated using the following formula:
Z_{base}=\frac{{kV_{base}}^2}{S_{base MVA}} Ohms…..(1)
For T-Line 1: Z_{base}=\frac{(220)^2}{100}= 484 Ohms
For T-Line 2: Z_{base}=\frac{(110)^2}{100}= 121 Ohms
For 3-phase load: Z_{base}=\frac{(11)^2}{100}= 1.21 Ohms
Step 4: Calculate the per unit impedance
The per unit impedance is calculated using the following formulas:
Z_{p.u.}=\frac{Z_{actual}}{Z_{base}} …..(2)
Z_{p.u._{new}}=Z_{p.u._{old}}(\frac{S_{base_{new}}}{S_{base_{old}}})(\frac{V_{base_{old}}}{V_{base_{new}}})^2 …..(3)
The voltage ratio in equation (3) is not equivalent to the transformers voltage ratio. It is the ratio of the transformer’s voltage rating on the primary or secondary side to the system nominal voltage on the same side.
For T-line 1 using equation (2): X_{l1_{p.u.}}=\frac{48.4}{484}= 0.1 pu
For T-line 2 using equation (2): X_{l2_{p.u.}}=\frac{65.43}{121}= 0.5 pu
For 3-Phase load:
Power Factor: \cos^{-1}(0.6)=\angle{53.13}
Thus, S_{3\phi}(load)=57\angle{53.13}
Z_{act}=\frac{(V_{rated})^2}{\overline{S}^*}= \frac{10.45^2}{57\angle{-53.13}}= 1.1495+j1.53267 Ohms
Per unit impedance of 3-phase load using equation (2)= \frac{1.1495+j1.5326}{1.21} = 0.95+j1.2667 pu
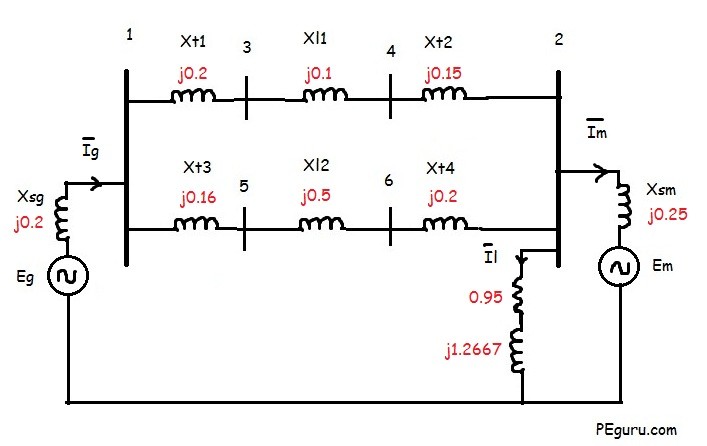
For generator, the new per unit reactance using equation (3)
X_{sg}= 0.18(\frac{100}{90})(\frac{22}{22})^2= 0.2 pu
For transformer T1: X_{t1}= 0.1(\frac{100}{50})(\frac{22}{22})^2 = 0.2 pu
For transformer T2: X_{t2}= 0.06(\frac{100}{40})(\frac{220}{220})^2 = 0.15 pu
For transformer T3: X_{t3}= 0.064(\frac{100}{40})(\frac{22}{22})^2 = 0.16 pu
For transformer T4: X_{t4}= 0.08(\frac{100}{40})(\frac{110}{110})^2 = 0.2 pu
For Motor, X_{sm}= 0.185(\frac{100}{66.5})(\frac{10.45}{11})^2 = 0.25 pu
Per Unit System Ebook
If you think you learned something today then you will love the eBook I prepared for you. It has 10 additional and unique per unit problems. Go ahead, preview it on the right. Get the complete version for only $1.00. Thanks for supporting this blog.
Per Unit Systems: Ten Total Problems Solved With Detailed Explanation Aleen Mohammed
- Per unit systems is an important concept in power system analysis. So much so, it shows up in all exams pertaining to power. Besides being taught in higher education, it is quite commonly used by engineers in the power industry. Equipment impedances are furnished in per unit. Source impedance for fault analysis is furnished in per unit. In this book, you will find enough problems solved for you to get the hang of this subject.
To view full load amps due to motor load and inductive load at Bus 2, see this post.
Summary
- Assume a Sbase for the entire system.
- The Vbase is defined by the transformer and any off-nominal tap setting it may have.
- Zbase is derived from the Sbase and Vbase.
- The new per unit impedance is obtained by converting the old per unit impedance on old base values to new ones. See equations (2) and (3).




Pingback: Per Unit System: Problem Solved For Easy Understanding (continued) | PEguru
It is given in the question that load is three phase then why didn’t you draw three phase RL load in the impedance diagram
I like it
Can I use the KVA of one of the transformers as the base instead of 100 MVA?Also, what if the Xpu value is not given as part of the question? In most questions, we the transformer KVA, Z% and primary and secondary voltage.
Yes you can use transformer KVA base for the system. You need to normalize the impedances of other equipment in the system using this new base.
Impedance value is hard to get. Only after the transformer is built and tested …. do you get the value. I think IEEE lists typical impedances for a standard transformer. But that’s a big assumption and you’ll need to state it clearly.
Please can you prove the change of base formula
Please kindly assist with the cable schedule for a 15MW,11KV gas turbine generating set to the switching substation. The distance is 4.5km putting into consideration 15%
I like to be in contact. Do you offer PE Electrical (Power) classes?
Can someone help please how can i calculate R and X from p.u. to base units?