Fundamental to any power system analysis is the know-how of per unit systems. This metric is widely used to describe voltages, currents, and impedances in a power system. This article, supplemented by an example, will explain step by step how to calculate these parameters for any component anywhere in the power system. Let’s begin with the purpose.
Purpose
1. Transformers and per unit systems
The reason the per unit system is employed is because it simplifies calculation of currents. Imagine a 3-phase system with a generator, a transformer, a T-line, another transformer, and a load. Every time you cross the transformers, the currents and voltages change. The impedance of the transformer referred to the primary side is different from the impedance of the same transformer referred to the secondary side. It is imperitive to use the appropriate impedance based on which side of the transformer you are on, which if not accounted for, introduces serious calculation errors.
Using actual values are fine if not for the transformers. They complicate matters. Generators and motors, like transformers, have different impedance when referred to either stator or rotor winding.
Deriving a per unit impedance values for these components enables easy calculation. This is because the per unit value remains the same whether you are on the primary side or the secondary side of the equipment.
Here’s an example from Eaton that solves a problem and explains this aspect in depth.
2. The \sqrt3 factor
The second factor in choosing per unit systems is the avoidance of \sqrt3 factor in the calculations. If you have ever tried calculating either the sending end voltage or the receiving end voltage in a system, you would know how important it is to factor in the \sqrt3 multiplier. This is because the voltages are always specified in phase to phase (L-L) values while the voltage drop across the impedances are calculated on per phase (L-N) basis. You will have to use \sqrt3 factor extensively to switch between L-L and L-N values.
When using the per unit system, a 3-phase balanced network is reduced to a 1-phase equivalent where the \sqrt3 isn’t even in the picture. So have fun calculating stuff.
3. Intuition enabler
The third factor is the meaning expressed by the per unit values. Look at the figure below.
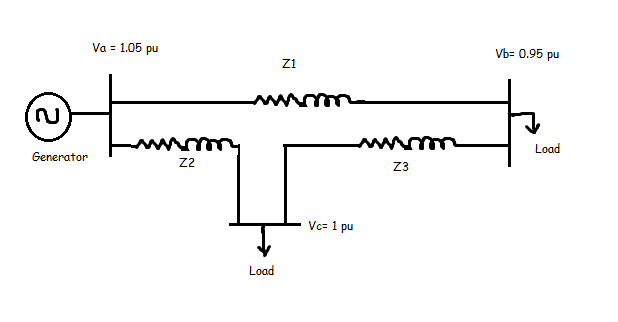
Figure 1: Voltage Per Unit
What does it tell about the system voltage profile? The generator is generating 5% above rated voltage. The load at bus C has no drop in voltage (1 pu) while the load at bus B sees 5% drop in voltage. Essentially, the voltage drops as you move away from the generator and closer to the load. It is easier to visualize this using per units than using actual values since the per unit values are normalized.
Also, someone with experience knows what the per unit values, especially impedance, of certain transformers or other devices in the system could be. It is easier for him or her to analyze the system by making reasonable assumptions.
Other factors for employing per unit system include
- enables the use of symmetrical components.
- widely used by manufacturers to specify their equipment – making it easy for direct analysis.
At this point it is suffice to say the per unit system is indispensable in analyzing the power system.
What is a per unit value?
The per unit of any quantity, be it voltage, current, or impedance is given by the following equation:
PerUnit_{quantity} = \frac{ActualValue_{quantity}}{BaseValue_{quantity}}Pretty straight forward equation. You have your actual value that you are trying to convert and a base value that is calculated from the given quantities like apparant power (S) and system voltage (V).
Sample per unit problem solved: https://peguru.com/2011/06/per-unit-system-practice-problem-solved-for-easy-understanding/

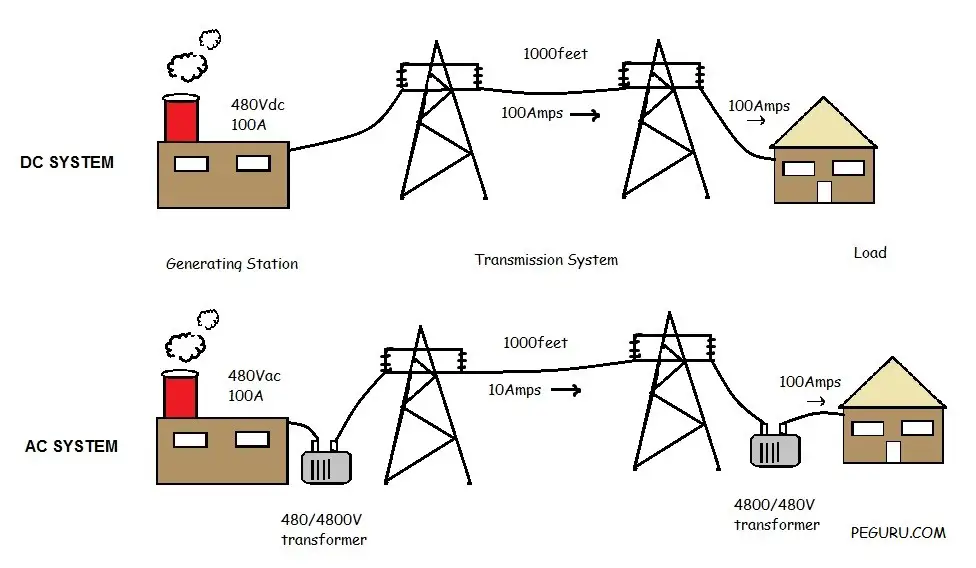
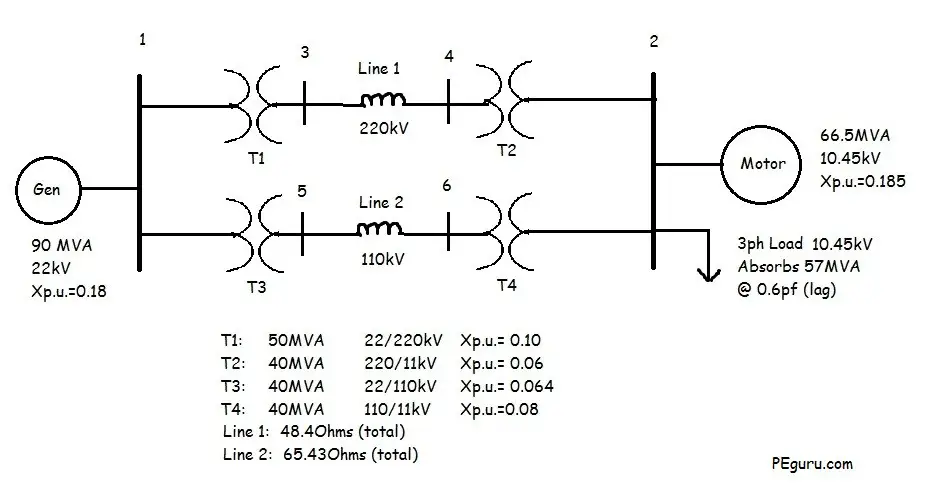



what is per unit droop in power system operation and control
Need to understand more of per unit