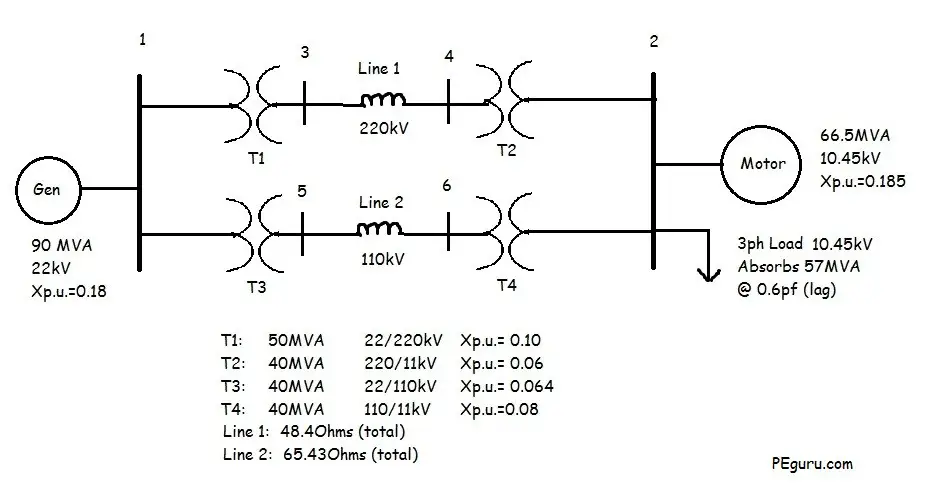
Let’s understand the concept of per unit system by solving an example. In the one-line diagram below, the impedance of various components in a power system, typically derived from their nameplates, are presented. The task now is to normalize these values using a common base.
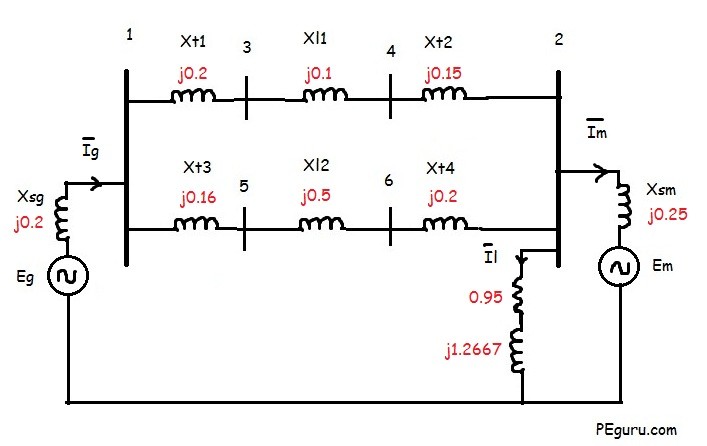
Now that you have carefully examined the system and its parameters, the equivalent impedance diagram for the above system would look something like the following.
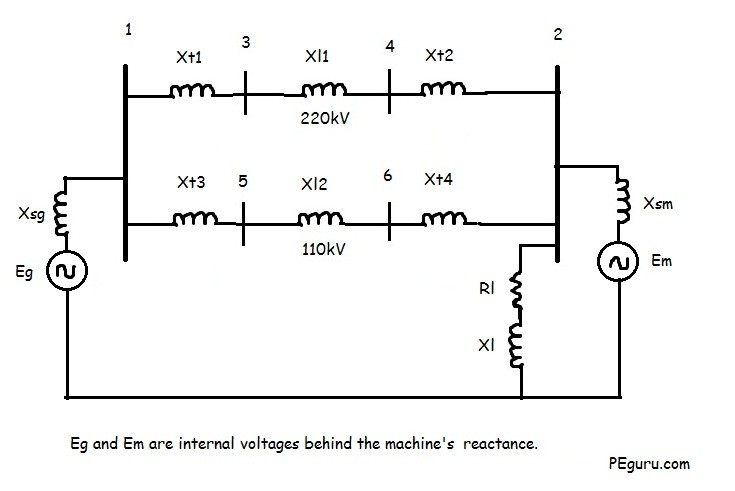
Resistive impedance for most components have been ignored. Rotating machines have been replaced with a voltage source behind their internal reactance. Capacitive effects between lines and to ground are ignored as well.
To obtain the new normalized per unit impedances, first we need to figure out the base values (Sbase, Vbase, Zbase) in the power system. Following steps will lead you through the process.
Step 1: Assume a system base
Assume a system wide S_{base} of 100MVA. This is a random assumption and chosen to make calculations easy when calculating the per unit impedances.
So, S_{base} = 100MVA
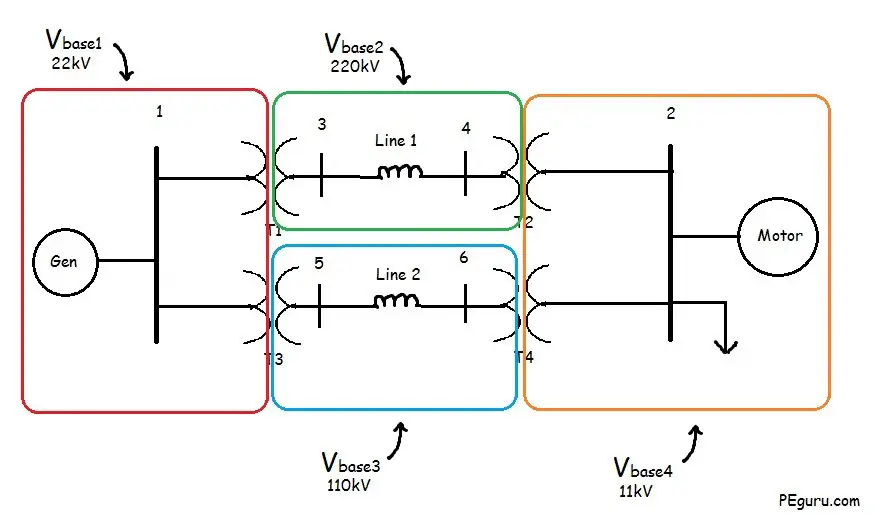
Step 2: Identify the voltage base
Voltage base in the system is determined by the transformer. For example, with a 22/220kV voltage rating of T1 transformer, the V_{base} on the primary side of T1 is 22kV while the secondary side is 220kV. It does not matter what the voltage rating of the other components are that are encompassed by the V_{base} zone.
See figure below for the voltage bases in the system.
Step 3: Calculate the base impedance
The base impedance is calculated using the following formula:
Z_{base}=\frac{{kV_{base}}^2}{S_{base MVA}} Ohms…..(1)
For T-Line 1: Z_{base}=\frac{(220)^2}{100}= 484 Ohms
For T-Line 2: Z_{base}=\frac{(110)^2}{100}= 121 Ohms
For 3-phase load: Z_{base}=\frac{(11)^2}{100}= 1.21 Ohms
Step 4: Calculate the per unit impedance
The per unit impedance is calculated using the following formulas:
Z_{p.u.}=\frac{Z_{actual}}{Z_{base}} …..(2)
Z_{p.u._{new}}=Z_{p.u._{old}}(\frac{S_{base_{new}}}{S_{base_{old}}})(\frac{V_{base_{old}}}{V_{base_{new}}})^2 …..(3)
The voltage ratio in equation (3) is not equivalent to the transformers voltage ratio. It is the ratio of the transformer’s voltage rating on the primary or secondary side to the system nominal voltage on the same side.
For T-line 1 using equation (2): X_{l1_{p.u.}}=\frac{48.4}{484}= 0.1 pu
For T-line 2 using equation (2): X_{l2_{p.u.}}=\frac{65.43}{121}= 0.5 pu
For 3-Phase load:
Power Factor: \cos^{-1}(0.6)=\angle{53.13}
Thus, S_{3\phi}(load)=57\angle{53.13}
Z_{act}=\frac{(V_{rated})^2}{\overline{S}^*}= \frac{10.45^2}{57\angle{-53.13}}= 1.1495+j1.53267 Ohms
Per unit impedance of 3-phase load using equation (2)= \frac{1.1495+j1.5326}{1.21} = 0.95+j1.2667 pu
For generator, the new per unit reactance using equation (3)
X_{sg}= 0.18(\frac{100}{90})(\frac{22}{22})^2= 0.2 pu
For transformer T1: X_{t1}= 0.1(\frac{100}{50})(\frac{22}{22})^2 = 0.2 pu
For transformer T2: X_{t2}= 0.06(\frac{100}{40})(\frac{220}{220})^2 = 0.15 pu
For transformer T3: X_{t3}= 0.064(\frac{100}{40})(\frac{22}{22})^2 = 0.16 pu
For transformer T4: X_{t4}= 0.08(\frac{100}{40})(\frac{110}{110})^2 = 0.2 pu
For Motor, X_{sm}= 0.185(\frac{100}{66.5})(\frac{10.45}{11})^2 = 0.25 pu
Per Unit System Ebook
If you think you learned something today then you will love the eBook I prepared for you. It has 10 additional and unique per unit problems. Go ahead, preview it on the right. Get the complete version for only $1.00. Thanks for supporting this blog.
Per Unit Systems: Ten Total Problems Solved With Detailed Explanation Aleen Mohammed
- Per unit systems is an important concept in power system analysis. So much so, it shows up in all exams pertaining to power. Besides being taught in higher education, it is quite commonly used by engineers in the power industry. Equipment impedances are furnished in per unit. Source impedance for fault analysis is furnished in per unit. In this book, you will find enough problems solved for you to get the hang of this subject.
To view full load amps due to motor load and inductive load at Bus 2, see this post.
Summary
- Assume a Sbase for the entire system.
- The Vbase is defined by the transformer and any off-nominal tap setting it may have.
- Zbase is derived from the Sbase and Vbase.
- The new per unit impedance is obtained by converting the old per unit impedance on old base values to new ones. See equations (2) and (3).




awesome
its really bcoz by reading this my confusion abut selection of base nd other is very clear…sommust read it frend /…thank u
@Pavan @Mike: That’s a typo. Correct values are now shown in the calculations. Since the ratio of Vbase_old/Vbase_new is the same, the end result, therefore, does not change. Appreciate the feedback.
This is really helpful. I didn’t really got it when reading through this, but when I saw the below comment by Mike, it seems like a question worth answering. However the content is really clear and understandable. Keep up the good work!
Thanks,
I don’t understand one part: When calculating Xtl2 you are using (22/22) which is reflected from where? Vbase in T2 is 220 primary and 11 secondary, so where does 22 come from?
The same for Xtl4.
will the impedance or p.u impedance in each line will be like in series? will the current for the PRIMARY AND SECONDARY of the transformer now be equal??? how will i find the actual line current for each line and for the whole system…
A single phase ,350 kva, 1380v generator has an internal impedance Zg of j6 ohms. The generator is used to supply a load of 250kva/440v at power factor 0.78 lagging. determine: the turns ratio of the transfomer, the impedance per km if the line between the generator and the transformer is 5km, the voltage regulation of the system.
Using the ratings of the generator as base values determine the generated per unit voltage that is required to produce a full load current under short circuit condition.
CAN SOMEONE HELP ME WIT THESE CALCULATION PLZ!!!
Kam,
Once you have the impedance network, use the current division rule to determine the current flowing each line. I am not sure I understand “voltage at 3”, if bus 3 is faulted (3ph) then it is zero otherwise it should be the same as nominal voltage as seen on the secondary side of the transformer.
I will solve one for the currents in the future but for now, you will have to learn how to reduce a circuit (using KVL and KCL) to determine the currents.
sorry but i didnt get my reply yet, so could you pls help me out???????? thanks a lot
very well explained but could you pls show me how to calculate voltage and current in both lines, will be very greatful , thanks a lot……….