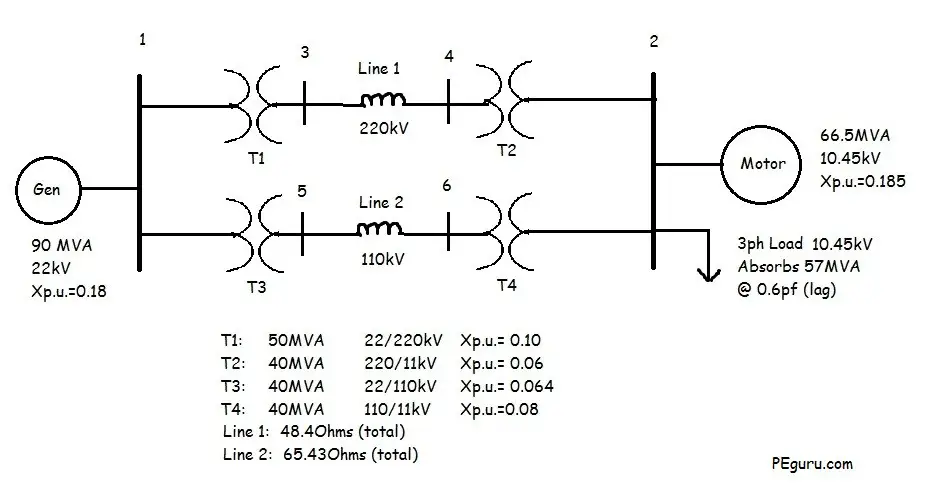
This post is a continuation of Per Unit System – Practice Problem Solved for Easy Understanding.
In the previous post, we calculated the per unit impedance of each equipment in the power system.
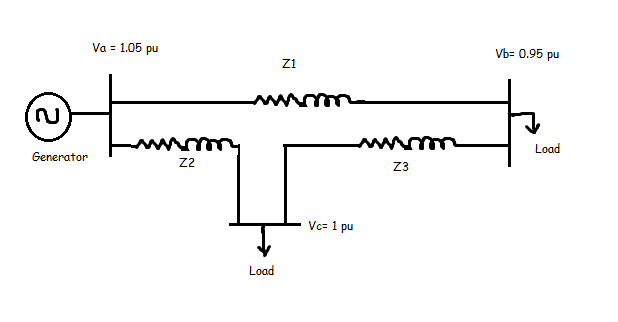
In this post we will calculate the full load amps at Bus 2. In the figure shown, Bus 2 is supplying the power to motor load and another inductive load. The available ratings of the load is also shown.
We need to assume the following before we get too far along
• Bus 2 is the reference bus. That is the phase angle will be 0.
• The motor has a leading power factor of 0.8.
Step 1: Calculate bus voltage
The per unit voltage at Bus 2 is
V_2=\frac{10.45}{11}\angle{0}=0.95\angle{0}
Step 2: Calculate current drawn by motor
The apparent power consumed by motor is
\overline{S_m}=\frac{66.5}{100}\angle{-36.87}
The current drawn by the motor is
\overline{I_m}=\frac{\overline{S_m^*}}{\overline{V_2}}=\frac{0.665\angle{36.87}}{0.95\angle{0}}= 0.56+j0.42
Step 3: Calculate current drawn by inductive load
Current drawn by load is
\overline{I_L}=\frac{\overline{V_2}}{\overline{Z_L}}=\frac{0.95\angle{0}}{0.95+j1.2667}=0.36-j0.48
Step 4: Calculate total current at Bus 2
Using KCL, the current in each leg equals the current entering at node Bus 2.
I.e. \overline{I}=\overline{I_m}+\overline{I_L}=0.92-j0.06 per unit
For current in Amperes, calculate
I_{base} = \frac{S_{base}}{V_{base}}=\frac{100,000,000}{11,000}=9,091Amps
8,382Amperes of load current is extremely high on single piece of bus. This happened because we added 66MVA AND 57MVA load on Bus 2. Note that this may not be a real world scenario.